Open Science Repository Mathematics

doi: 10.7392/Mathematics.70081907

On Determining a Circle that Optimally Packs Rectangles

Ayele Taye, Ph.D.

School of Mathematical and Statistical Sciences, Hawassa University

Abstract

This paper deals with a mathematical problem of determining a circle that can optimally pack a rectangle of known length and width. Theoretical relationship between length of the rectangle and radius of the circle is established. A numerical method is used to make estimations. The estimated functions seem to represent polynomials.

Keywords: circle, geometry, numerical method, rectangular pieces.

Introduction

The mathematical problem of interest is to find an economical possible circle that can accommodate a given set of rectangular pieces of a material having same width and known total length. An economical possible circle would mean that the rectangular pieces would optimally fit to or inscribe in the circle.

Let the total length be denoted by L, width by W and radius of the circle by R. Such problems may arise in reality, for example in engineering fields and arts. To mention one, suppose each rectangular piece stands for a character; alphabet or blank space or symbol. Then, given the total number of these characters, a practical question to be answered may be to determine the smallest possible circle in which all the characters can be written or drawn. The objective of the current work is, thus, to establish a simple relationship between length L of the rectangle and radius R of the required circle, for a given width W of the rectangle.

Methods

Given width W of the rectangular material, a theoretical relationship between length L and radius R of the intended circle will be developed. The function will be explored using numerical methods. This computation can easily be done on any computing software, such as Microsoft Excel. By plotting the computed paired values (L,R) on the RL axis, a known curve will be fitted to the scatter plots. The fitted curve, though approximation, would give a simple solution to the problem. Example will be considered for illustration.

Results

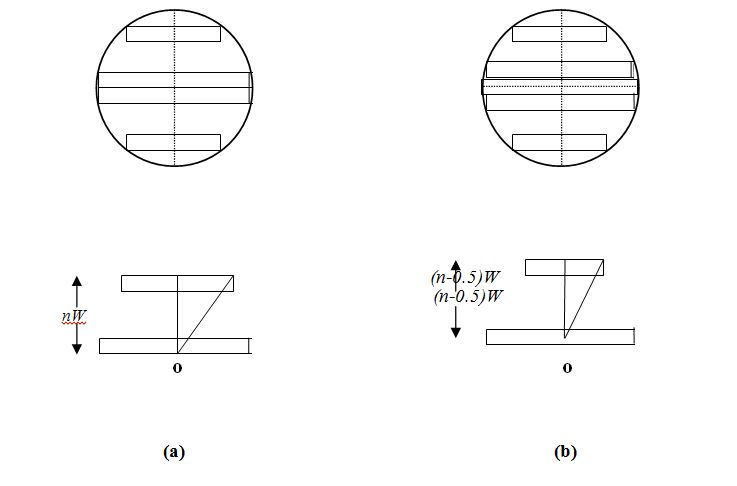
When trying to fit the rectangular pieces to the circle, new rectangular arrangements are formed (see Fig. 1a and Fig. 1b). The number of such rectangular arrangements that are fitted to the circle is either even or odd depending on the position of the center of the circle.

The number of such rectangular arrangements, denoted by N, is even when:

• Case 1: center of the circle lies on the edge of the rectangle (see Fig. 1a).

And odd when:

• Case 2: center of the circle lies at the center of the rectangle (see Fig. 1b).

Using the Pythagorean Theorem, the length of each arranged rectangle can be shown to:

for the n^th arranged rectangle above or below the center (Case 1); and

for the arranged rectangle at the center; and

for the (n-1)^th arranged rectangle above or below the center rectangle (Case 2).

The number of arranged rectangles in the circle should be N=[2R/W]; the greatest integer less or equal to the value of (2R/W). Since N/2 is integer when N is even and N/2-0.5 is integer when N is odd, the total length of all rectangular pieces should be the sum of the individual lengths given as:

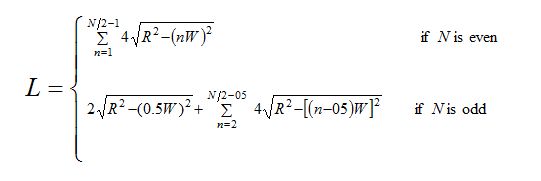
Where N ≥ 4 for Case 1 and N ≥ 5 for Case 2.

Expression (1) indicates that L can be expressed as a function of W and R. However, it is not easy to see how L and R are related as this summation cannot be analytically simplified. Thus numerical computation may help as considered in the following examples.

Special cases: Consider the case when W=1 cm. Since the number of arranged rectangles in the circle would be N=[2R/H]=[2R], L becomes a function of radius R only. Then expression (1) reduces to the form:

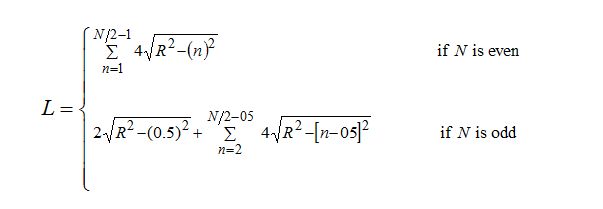
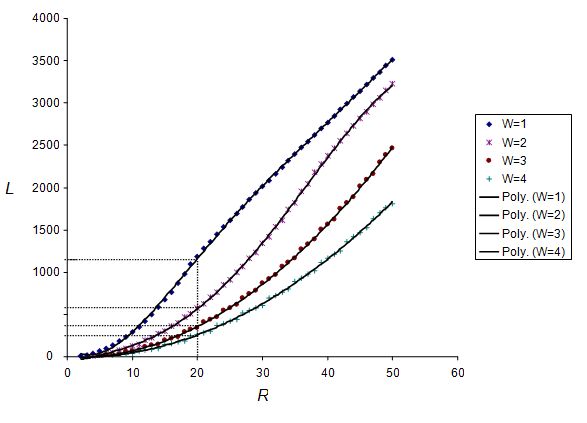
Similar derivations are done for the cases of W=2 cm, W=3 cm and W=4 cm. In each of the cases, L is computed at different values of R and plotted on the LR co-ordinates axis (see Fig. 2). The curves all look non-linear. By fitting polynomial curves (see Fig. 2), the respective approximations for the cases of W=1 cm, W=2 cm, W=3 cm and W=4 cm are found to be:

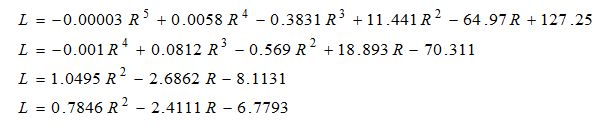
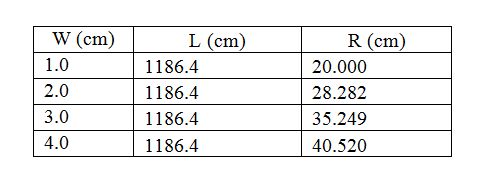
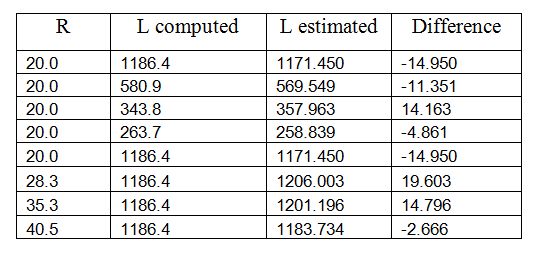
According to this computation, the smallest possible circle that can optimally accommodate the rectangular pieces of a material with total length of about 1186.4 cm and with same width equal to 1 cm should have a radius of about 20 cm. For example, a set of 1186.4 characters each of which has size 1 cm x 1 cm can be written or drawn in a circle of radius 20 cm. With width 2 cm, 3 cm and 4 cm, the required circles should have radii of about 28.282 cm, 35.249 cm and 40.520 cm respectively (see Table 1).

Table 1: Radius of the circle.

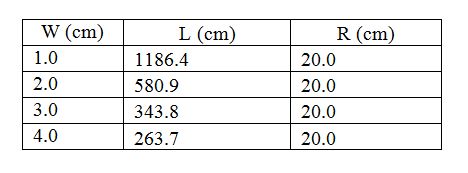
On the other hand, by fixing the radius of the circle to be 20 cm, one can optimally accommodate the rectangular pieces of total length 580.4 cm with width 2 cm or total length 343.8 cm with width 3 cm or total length 263.7 cm with width 4 cm (see Table 2).

Table 2: Radius of the circle.

The discrepancy of estimations by numerical method and the fitted polynomials (see Table 3) seems to vary, but can be minimized.

Table 3. Discrepancy between estimations.

Conclusion

Theoretical relationship between the total length of the rectangular pieces of the material and the radius of the required circle is established. Based on numerical computations and as shown in Fig. 2 and Fig. 3, for each width W of the rectangle, the length L of the rectangle increases with radius R of the required circle. However, the rate of increment decreases and also the inflection point moves upward with increasing W.

It may be interesting to note also that the coefficient of R² in the last two expressions seems to be related to W and p, since p/3 = 1.047198 and p/4 = 0.785398 are very much comparable to the corresponding coefficients 1.0495 and 0.7846.

It can be concluded from this work that given width of the rectangle, the relationship between the total length of the rectangular pieces of the material and the radius of the required circle to optimally accommodate seems to be a polynomial. The order of the polynomial gets lower as the width of the rectangle gets larger, and that the coefficient of R² (radius squared) seems to approach p/W for large width W. It is an open problem to find coefficients of the polynomials analytically or more accurately.

References

1. Rich, B. (2001). Schaum's Easy Outline of Geometry. McGraw-Hill Companies.

2. Thomas, D. A. (2002). Modern Geometry. Brooks/Cole.

Cite this paper

APA

Taye, A. (2012). On Determining a Circle that Optimally Packs Rectangles. Open Science Repository Mathematics, Online(open-access), e70081907. doi:10.7392/Mathematics.70081907

MLA

Taye, Ayele. “On Determining a Circle That Optimally Packs Rectangles.” Open Science Repository Mathematics Online.open-access (2012): e70081907.

Chicago

Taye, Ayele. “On Determining a Circle That Optimally Packs Rectangles.” Open Science Repository Mathematics Online, no. open-access (November 26, 2012): e70081907. http://www.open-science-repository.com/on-determining-a-circle-that-optimally-packs-rectangles.html.

Harvard

Taye, A., 2012. On Determining a Circle that Optimally Packs Rectangles. Open Science Repository Mathematics, Online(open-access), p.e70081907. Available at: http://www.open-science-repository.com/on-determining-a-circle-that-optimally-packs-rectangles.html.

Science

1. A. Taye, On Determining a Circle that Optimally Packs Rectangles, Open Science Repository Mathematics Online, e70081907 (2012).

Nature

1. Taye, A. On Determining a Circle that Optimally Packs Rectangles. Open Science Repository Mathematics Online, e70081907 (2012).

doi

DOI name: 10.7392/Mathematics.70081907

This work is licensed under a Creative Commons Attribution 3.0 Unported License.

Export to Mendeley