Open Science Repository Economics
doi: 10.7392/Economics.70081922
Fluctuation of Crude Oil Prices at the International Level: Application of Dynamic and Discrete Stochastic Models
School of Mathematical and Statistical Sciences, Hawassa University
Abstract
Most energy-consuming economic activities in the world are dependent on the energy source from crude oil. And one of the characteristics of the price of crude oil is its high scale of wavering that can directly or indirectly affect the economic progress of both oil exporter and importer nations. The main aim of this study is to assess the fluctuations of monthly average price of crude oil and its shock at the international market using the daily recorded data from 1st Jan 2003 to 30th Nov 2011 from OPEC. Autoregressive Moving Average model with exogenous inputs model (ARMAX) is used as an empirical model. The result of the study reveals that the ARMAX (2,0) discrete stochastic model captures the fluctuation of the log-transformed monthly mean price with exogenous inputs of annual-time specific effects. This shows that, once the price of the crude oil is set, its effect goes up to two months. In normal conditions we expect that the price shock is higher at higher price of the commodity. However, astonishingly, the monthly average price of crude oil and the price shock at the international market are found to be uncorrelated. The ARIMAX (2,2,1) discrete stochastic model captures the fluctuation of the log-transformed price shock on crude oil with harmonic variations of sine wave of amplitude $1.35 month after month. In general, the problem of handling the fluctuation of the price of crude oil at the international market is not only attributed to unorthodoxies from the mean but also to problems of price shocks emanating from unknown factors from either exporters or importer nations.
Keywords: Galton distribution, price of crude oil, price shock, ARMAX models.
Citation: Yebabe, Y. (2013). Fluctuation of Crude Oil Prices at the International Level: Application of Dynamic and Discrete Stochastic Models. Open Science Repository Economics, Online(open-access), e70081922. doi:10.7392/Economics.70081922
Received: December 31, 2012.
Accepted: January 28, 2013.
Published: January 31, 2013.
Copyright: © 2013 Yohannes Yebabe. Creative Commons Attribution 3.0 Unported License.
Contact: [email protected]
Introduction
Background
Technologically advanced societies have become increasingly dependent on peripheral energy sources for transportation, the production of many manufactured goods and the conveyance of energy services. Globally, energy consumption grew more rapidly than the global economy, meaning that the energy intensity of economic activity increased. The energy markets have pooled crisis recovery and strong industry dynamism. Therefore, each nation in the world faces the challenge to achieve rapid economic development and sustainable supply of energy. Many economists mentioned that there is strong interdependence between the volume of energy consumption and economic development of a given nation. Whenever the energy consumption of a given nation is high, it is observed that the GDP of that nation somehow showed a positive change (Jaruwan Chontanawat et al, 2006).
Among the principal energy sources of the world, oil is the largest (above 33%) and its prices have increased dramatically. Succeeding to oil, coal posed a budding role in the world's energy consumption. For instance, in 2008, coal accounted nearly for 27% of the other energy sources of the world. The other energy sources of the world in descending order are gas, nuclear power, hydroelectric power and others like geothermal power, solar energy, and bio-fuel (Survey of Energy Resources, 2010).
The vulnerability of higher oil prices on the oil importer nations
Oil prices tranquility matters to the health of the world economy. However, the structures of the price of oil in these recent times have exhibited exceptional volatility. Higher oil prices are recorded since 1999 -partly the results of OPEC supply-management policies- and contributed to the global economic recession in 2000-2001, dampening the current cyclical upturn (Paul Stevens, 2005). These higher prices are contributing to stubbornly high levels of unemployment and exacerbating budget deficit problems in many OECD and other oil-importing nations (IEA, 2010). The vulnerability of oil-importing nations to higher oil prices varies is evidently contingent on the degree to which they are net importers and the oil intensity of their economies. Higher oil prices cause inflation on food prices to nurture by some percentage point. Euro-zone nations would suffer most in the short term, their GDP dropping by 0.5% and inflation rising by 0.5% in 2004. In the same year the United States would suffer the least, with GDP falling by 0.3% and Japan’s GDP would fall 0.4 % (Paul Stevens, 2005) and Yu Hsing, 2009).
The antagonistic economic impact of higher oil prices on oil-importing developing nations is generally even more severe than for OECD nations. This is because their economies are more dependent on imported oil and more energy-intensive and because energy is used less efficiently (TWAS, 2008). India spent $15 billion, equivalent to 3% of its GDP, on oil imports in 2003, which is 16% higher than its 2001 oil-import bill. In 2004 the loss of GDP averages 0.8% in Asia and 1.6% in very poor highly-indebted nations in the year following a $10 oil-price increase. In the same year, the loss of GDP in the Sub-Saharan African nations would be more than 3% (Mary S. Fowler and Joseph B. Kadane, 2006).
Some known factors affecting the price of crude oil
According to the Energy Information Administration (2007), crude oil prices have increased and showed dramatic fluctuations in latest years. Many economists (Abdoulkarim Esmaeili and Zainab Shokoohi, 2011, E.S. Dokuchaev et al., 2006, Deren Unalmis et al., 2009, H. Mostafaei and L. Sakhabaksh, 2011, etc.) claim that the important factors which can affect the global price of the crude oil are:
- Global changes in supply by OPEC and demand by oil importer nations like US, China and European countries.
- Crude oil prices are dependent on the sentiments of the global equity market. Moreover, Dow Jones Industrial Average Index, NASDAQ and NYSE are few which governs the US equity market and hence the oil prices as well.
- The movement in Dollar index also changes the oil prices on daily basis. When dollar goes up, oil prices go down and vice versa.
- The US Labour Department also comes out with unemployment report which conveys the unemployment rate in US (negatively correlated with crude oil price).
- Wars, geopolitical crises, recession and natural disaster are some other important factors that also momentously affect oil prices.
Oil markets have been drawing increased interest and participation from investors and financial entities without direct commercial involvement in physical oil markets. The role of these non-commercial futures market participants in recent price developments is challenging to assess, particularly over short time intervals (Kathleen King et al., 2012). Therefore, we need rigorous quantitative information about the primary explanation for the recent trend in oil prices. Therefore, main motivation of the study is to apply the dynamic discrete stochastic models to capture the fluctuations of monthly average price with its price shock of crude oil at the international market.
Objectives
The major prominence of this study is to develop econometric model seizure of the fluctuation of the monthly average price of crude oil and the price shock within the month, by applying the Autoregressive Moving Average with exogenous input (ARMAX) model. The specific objectives are:
- To assess whether there is a specific probability distribution for the daily price of crude oil by annual discretization or not.
- To assess the impact of the annual time specific effects on the monthly mean price of crude oil.
- To assess whether the price shock is interrelated with monthly average price of the crude oil or not.
- To compare the randomness of the monthly mean price of crude oil and the price shock on crude oil within the month.
Data
The study used secondary data obtained from OPEC for the period between Jan 1, 2003 and Dec 20, 2011.
Variables
Exogenous variables: (1) annual time specific effects (TE): these include overall factors indicated in section "Some known factors affecting the price of crude oil" above that appeared in each year. (2) the sine and cosine waves over time.
Dependent (endogenous) variables: (1) the price shock on the crude price within the month (Ps). And (2) the monthly average price of crude oil (Pr).
Methodology
General assumptions
The general assumption for our analysis is that both the monthly average price and the price shock within the month of the crude oil at the international market are continuous random variables.
Sampling design
Judgment sampling: Judgment sampling is a type of non-random sampling, which is selected based on the opinion of an expert. When it comes to the sampling process, it is usually biased since no randomization is used in obtaining the sample. It is also worth noting that the members of the population did not have equal chances of being selected. This type of sampling technique is also known as purposive sampling (Doherty, M., 1994).
Models
The Galton distribution: The Galton distribution frequently named as log-normal distribution is a probability distribution of a random variable whose logarithm is normally distributed. In other words, if X is a random variable with a normal distribution, then Y = exp(X) has a log-normal distribution (Ken Johnston and Elton Scott (1997) and Eckhard Limpert (2001)).Since
where the parameters denoted μ and σ, are the mean and standard deviation.
Autoregressive moving average with exogenous inputs (ARMAX) model: The notation ARMAX (p,q,b) refers to the model with p autoregressive terms, q moving average terms and b exogenous inputs terms. This model contains the AR(p) and MA(p) models and a linear amalgamation of the last b terms of a known and external time series dt. It is given by A. Ouakasse and G. Melared, 2009:
where
Parameter estimation and model fitting: For the ARMAX model the parameter estimation is based on the Melard’s algorism (A. Ouakasse and G. Melared, 2009). Finding appropriate values of p and q in the ARMA(p,q) model can be facilitated by plotting the partial-autocorrelation functions for determining p, and likewise using the autocorrelation functions for determining q.
Criteria of best model selection
Akaike information criterion (AIC): AIC is a measure of the relative goodness of fit of a statistical model. It is grounded in the concept of information entropy, in effect offering a relative measure of the information lost when a given model is used to describe reality. AIC is defined as:Bayesian information criterion (BIC): The AIC penalizes the number of parameters less strongly than does the BIC. The BIC is an asymptotic result derived under the assumptions that the data distribution is in the exponential family. The formula for the BIC is given as:
The Cochrane-Orcutt recursive estimation: Cochrane-Orcutt estimation is a procedure in econometrics, which adjusts a linear model for serial-correlation in the error term. Suppose we have a linear econometric model given as
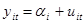 , i=1,2…a, t=1,2,….T (7), where
, i=1,2…a, t=1,2,….T (7), where 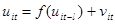 is serially correlated random
error term,
is serially correlated random
error term, 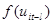 is the functional
structure of the serial correlation,
is the functional
structure of the serial correlation, 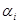 is
the ith effect on
is
the ith effect on Results
Econometric framework for problem decomposition
Assessing the existence of specific probability distribution of the daily prices of crude oil
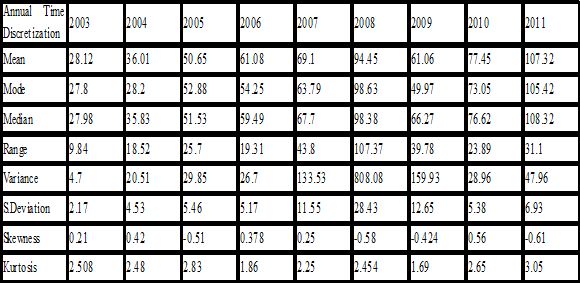
At this point we apply the judgement sampling technique that we targeted on the daily prices of crude oil by annual discretization. In demand to characteristics of our random variable, we have to analyze the sample statistic. Witnessing the sample information about the daily prices of crude oil will help us to decide whether these random values come from a certain probability distributions or not. Table 1 helps us to characterize the natures of the parameters of the daily price of crude oil.
Table 1: Descriptive statistical information about the price of crude oil by annual discretization.
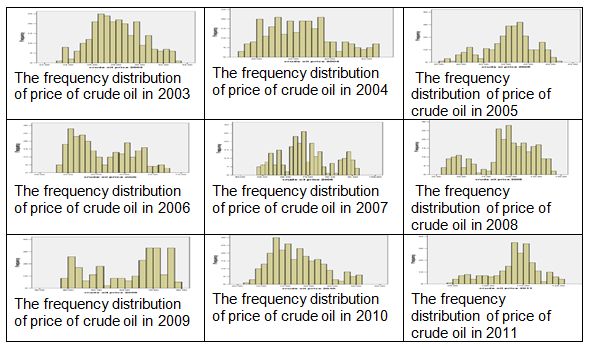
The sample statistic suggests that the measures of central tendencies and range and standard deviations are time variant. This shows that the price of the crude oil has its own structure in each fiscal year. From this fact we can conclude that the daily prices of crude oil by annual discretization do not come from some specific probability distribution. In other words, we cannot find a specific probability distribution function for the daily price of crude oil by annual discretization. Moreover, the following Figure 1 concretizes our argument.
Figure 1: Frequency distributions of the daily price of crude oil by annual discretization.
Therefore, this evidence will tell us, contrasting the research paper by Haiyan Xu et al. (2011), that Galton probability distribution is not the specific probability distribution of the daily price of crude oil at the international market. The implications of the absence of specific probability distribution function to the daily price of crude oil to the oil-importer nations is strong exertion of scheduling annual budget to import it. In our succeeding analysis we rent asunder the variation of the daily price of crude oil in monthly average prices and price shock within the month.
Modeling the monthly average price of crude oil
At this juncture we can use the concept of the Laws of Large numbers and the CLT in mandate to assume the random error terms follow multivariate normal distributions. The econometric model that we are going to fit is given as:
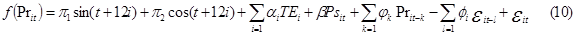
where:
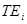 = the ith annual
time-specific effect from 2003-2011 on the price of crude oil Psit
is the price shock on crude oil in ith year and in tth
month, Prit is the monthly average price of crude oil in ith
year and in tth month. The sine and the cosine waves are the
harmonic regression components,
= the ith annual
time-specific effect from 2003-2011 on the price of crude oil Psit
is the price shock on crude oil in ith year and in tth
month, Prit is the monthly average price of crude oil in ith
year and in tth month. The sine and the cosine waves are the
harmonic regression components, 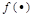 is a
mathematical transformation function of Prit and
is a
mathematical transformation function of Prit and  .
.
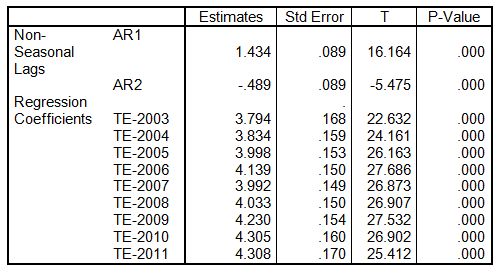
After comparing different ARMAX models, we found that the log-transformed monthly average price of crude oil is best fitted by the ARMAX(2,0) model. Table 2 can give the estimates of the model parameters.
Table 2: The estimated parameters of the Log-transformed monthly average price of the crude oil using model.
Economic interpretations of the results of Table 2
Each annual time-specific effect is strongly associated with the log-monthly average price of the crude oil. From 2003-2006, the US-Iraq war plays important role on the raise of the monthly average price of crude oil. The war directly increases the monthly average price of crude oil in the years 2004-2006 (as we see from the table, the estimated model parameters of the annual time-specific effects are statistically increasing with time). This result argues with researchers like Paul Stevens (2005), R.G. Cong et al., (2008), and Lutz Kilian (2009). In normal conditions, we expect that the price shock on the item is higher at higher prices of the commodity. However, astonishingly, the monthly average price of crude oil and the price shock at the international market are uncorrelated. This will give us evidence that the increment of the monthly average prices of crude oil cannot intensify the price shock or the vice versa.
The AR (2) process is the stochastic part significant to the current monthly average price of crude oil. This shows that, once the price of crude oil is set, it will influence the prices up to two months. Moreover, the harmonic parts of the regression are all insignificant, this demonstrating that both the sine and cosine waves are not observable as components of the fluctuations of the monthly average price crude oil.
Figure 2: The comparison of the fitted and observed values of the monthly average price of crude oil using the Log-transformed model.
From Figure 2 we see a remarkable fit that even it is problematic to differentiate the observed average monthly prices of the crude oil and the predicted values using the model. Therefore, unlike other research papers (H. Mostafaei, L. Sakhabaksh, 2011, Jun Wang et al. 2009), it is better to apply the ARMAX models to capture the fluctuations of the monthly average price of crude oil for prediction short memory prediction.
Developing the best fit of the fluctuations of the price shock on crude oil
By defining price shock is
the prices deviated from the monthly average price of crude oil, the model
which can capture the fluctuations of price shock on crude oil is given as:
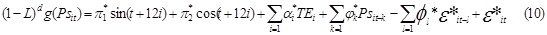
where: 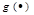 is the ith annual time specific effect from
2003-2011 on the price of crude oil, Psit is the
price shock on crude oil in ith year and in tth month. The sine and the cosine waves are the harmonic regression components, d is the appropriate differencing operator
is the ith annual time specific effect from
2003-2011 on the price of crude oil, Psit is the
price shock on crude oil in ith year and in tth month. The sine and the cosine waves are the harmonic regression components, d is the appropriate differencing operator 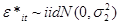 is
a mathematical transformation function of Psit and
is
a mathematical transformation function of Psit and 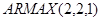 .
.
After comparing different
models, we found that the ARIMAX(2,2,1) model
is the best fit for the price shock on crude oil. Table 3 gives the estimates
of the model parameters.
Table 3: The estimated parameters of the Log-transformed price shock on the crude oil using ARIMAX(2,2,1) model.
Economic interpretation the results of Table 3
The AR (2) is statistically significant. This implies that once the fluctuation of the price shock on crude oil is initiated it will continue up to two months in similar magnitude of disturbance. The harmonic regression sine wave of amplitude $1.35 is observed as fluctuation component of price shock. However, there are no significant known exogenous inputs for the predictor of price shock on crude oil. This is evidence that the price shock on crude oil is more random than the monthly average price of crude oil.
Comparisons on the amplitudes of price shock on crude oil
In this section we try to compare the price shocks on crude oil by categorizing annual times that have similar amplitude of disturbances and using the autoregression. Table 4 will give us the estimated price shock recorded with in the category of time fixed effects.
Table 4: The estimates of the amplitudes of price shock on crude oil.
From Table 4 one can see that all the model parameters are significant. This implies that the world’s price shock of the crude oil has passed through five different categories over the last 9 years. The minimum price shock is recorded by the year 2003. This will tell us the price shocks were much stable within the year. The maximum price shock is recorded by the year 2008. This implies that the international market of the crude oil was much unstable in 2008. There are similar price shocks on the crude oil recorded from year 2004-2007 and from year 2009-2010.
Conclusions and recommendations
Conclusions
This paper tried to see whether the daily prices of crude oil by annual discretization follows a specific probability distribution or not. Based on the time-variant property of the important sample statistic as the estimates of the population parameters, we conclude that there is no specific probability distribution for the daily price of crude oil by annual discretization. Using discrete dynamic stochastic models on the newly introduced variables by splitting the variations of the daily prices of crude oil into monthly average price and price shock within the month, the paper found that the ARMAX(2,0) model capture the monthly price of crude oil and the ARMAX(2,2,1) stochastic model capture the amplitude of price shock on crude oil. Moreover, the monthly average price of crude oil is affected by many known factors (like war, the US economy, China and EU-nations) aggregately estimated by the specific-time effects. Nevertheless, the source and cause of price shock on crude oil are unknown factors.
A noteworthy result that the paper identified is that the source of price shock is not correlated with the increment of monthly average price of the crude oil. This is the evidence that the price shock on crude oil is undetermined to both the oil-exporter and the oil-importer nations. From this point of view, the regulations of the price of crude oil at the international market could not be achieved through negotiations and setting different agreements among the oil-importer and exporter nations. This is because of the structure of globalization, free market and expansion of privatization.
Recommendations
The price of crude oil in the international market is complete of stochastic type. This randomness is most likely being complicated as the world’s economic integration is more globalized This problem of has two major consequences on the oil-importer nations. If the economic dependence of the nations is strong, then they will rebalance their expenditure for oil by their revenue from export. In this case, either if the price of oil is increasing or not, the structure of the increment of the price of crude oil will most probably not affect the economy of the oil-importer nation. On the other hand, if the economy of the oil-importer nation is weak, then the nation’s expenditure of importing oil is most likely unbalanced by the revenue of the nation’s export. From this point of view, the raise of the price of crude oil most likely affects the GDP of oil importer developing nations. Therefore, especially oil-importer developing nations need the implementation of other energy sources like hydro-electric power, bio-fuel, solar energy, wind energy or others.
From the structural trend of the price of crude oil, it is observed that such price is showing rapid changes of fluctuations, because oil is the leading of the world’s source of energy. Therefore, each nation in the world should be focused on how to increase the share of the other energy sources. Once the share of crude oil is decreasing, its price and its price shock will be stabilized.
References
[1] A. Ouakasse and G. Melared (2009). A New Recursive Estimation Method for Single Input Single Output models. University Libre de Bruxelles. FIND ONLINE
[2] Esmaeili, A., & Shokoohi, Z. (2011). Assessing the effect of oil price on world food prices: Application of principal component analysis. Energy Policy, 39(2), 1022-1025. FIND ONLINE
[3] Unalmis, D., Unalmis, I., & Unsal, D. (2009). On the Sources of Oil Price Fluctuations. IMF Working Papers, 1-28. FIND ONLINE
[4] Doherty, M. (1994) Probability versus Non-Probability Sampling in Sample Surveys. The New Zealand Statistics Review. March 1994, pp 21-28. FIND ONLINE
[5] E.S. Dokuchaev, A.M Rogacheva and E.V. Evtushenko (2006), The Forecasting of the World Oil Price by Summing up Linear Trend and Periodic Functions. Intellectual Service for Oil and Gas Industry. Vol. IV. FIND ONLINE
[6] Limpert, E., Stahel, W. A., & Abbt, M. (2001). Log-normal distributions across the sciences: keys and clues. BioScience, 51(5), 341-352. FIND ONLINE
[7] Melard, G. (1984). Algorithm AS 197: A fast algorithm for the exact likelihood of autoregressive-moving average models. Journal of the Royal Statistical Society. Series C (Applied Statistics), 33(1), 104-114.FIND ONLINE
[8] H. Mostafaei and L. Sakhabaksh. (2011). Modelling and forecasting OPEC oil prices with AFRIMA model. International Journal of Academic Research.FIND ONLINE
[9] Haiyan Xu and Zhong Xiang Zhang (2011). A Trend Deduction Models of Fluctuating Oil Prices.Fondazione Eni Enrico Mattei. FIND ONLINE
[10] IEA, OPEC, OECD and World Bank Joint Report (2010). Analysis of the Scope of Energy Subsidizes and Suggestions for the G-20 Initiative. G-20 Summit Meeting Toronto. FIND ONLINE
[11] Chontanawat, J., Hunt, L. C., & Pierse, R. (2006). Causality between Energy Consumption and GDP: Evidence from 30 OECD and 78 non-OECD Countries.Surrey Energy Economics Centre (SEEC), School of Economics Discussion Papers (SEEDS). FIND ONLINE
[12] Dufour, J. M., Gaudry, M. J., & Liem, T. C. (1980). The Cochrane-Orcutt procedure numerical examples of multiple admissible minima. Economics Letters, 6(1), 43-48. FIND ONLINE
[13] Wang, J., Pan, H., & Liu, F. (2012). Forecasting Crude Oil Price and Stock Price by Jump Stochastic Time Effective Neural Network Model. Journal of Applied Mathematics, 2012. FIND ONLINE
[14] Katelijne A.E. Carbonez. (2008). Model Selection and Estimation of Long-Memory Time-Series Models. Katholiek Universiteit Leuven. FIND ONLINE
[15] Kathleen King, Ai Deng, and David Metz. (2012). An Econometric Analysis of Oil Price Movements: The Role of Political Events and Economic News, Financial Trading, and Market Fundamentals. Bates White. FIND ONLINE
[16] Kilian, L. (2010). Explaining fluctuations in gasoline prices: a joint model of the global crude oil market and the US retail gasoline market. Energy Journal,31(2), 87. FIND ONLINE
[17] Fowler, M. S., & Kadane, J. B. (2006). Oil and Gas on Indian Reservations: Statistical Methods Help to Establish Value for Royalty Purposes. J. Stat. Educ., 14, 3. FIND ONLINE
[18] Farzanegan, M. R., & Markwardt, G. (2009). The effects of oil price shocks on the Iranian economy. Energy Economics, 31(1), 134-151. FIND ONLINE
[19] Stevens, P. (2005). Oil markets. Oxford Review of Economic Policy, 21(1), 19-42. FIND ONLINE
[20] Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica: Journal of the Econometric Society, 987-1007. FIND ONLINE
[21] Cong, R. G., Wei, Y. M., Jiao, J. L., & Fan, Y. (2008). Relationships between oil price shocks and stock market: An empirical analysis from China. Energy Policy, 36(9), 3544-3553. FIND ONLINE
[22] Survey of Energy Resources. (2010). World Energy Council, London. FIND ONLINE
[23] TWAS. (2008). Sustainable energy for Developing Countries, Academy of Sciences for the Developing World. FIND ONLINE
[24] Hsing, Y. (2007). Impacts of higher crude oil prices and changing macroeconomic conditions on output growth in Germany. International Research Journal of Finance and Economics, 11, 134-140. FIND ONLINE
Cite this paper
APA
Yebabe, Y. (2013). Fluctuation of Crude Oil Prices at the International Level: Application of Dynamic and Discrete Stochastic Models. Open Science Repository Economics, Online(open-access), e70081922. doi:10.7392/Economics.70081921
MLA
Yebabe, Yohannes. “Fluctuation of Crude Oil Prices at the International Level: Application of Dynamic and Discrete Stochastic Models.” Open Science Repository Economics Online.open-access (2013): e70081922. Web. 31 Jan. 2013.
Chicago
Yebabe, Yohannes. “Fluctuation of Crude Oil Prices at the International Level: Application of Dynamic and Discrete Stochastic Models.” Open Science Repository Economics Online, no. open-access (January 31, 2013): e70081922. http://www.open-science-repository.com/fluctuation-of-crude-oil-prices-at-the-international-level.html.
Harvard
Yebabe, Y., 2013. Fluctuation of Crude Oil Prices at the International Level: Application of Dynamic and Discrete Stochastic Models. Open Science Repository Economics, Online(open-access), p.e70081922. Available at: http://www.open-science-repository.com/fluctuation-of-crude-oil-prices-at-the-international-level.html.
Science
1. Y. Yebabe, Fluctuation of Crude Oil Prices at the International Level: Application of Dynamic and Discrete Stochastic Models, Open Science Repository Economics Online, e70081922 (2013).
Nature
1. Yebabe, Y. Fluctuation of Crude Oil Prices at the International Level: Application of Dynamic and Discrete Stochastic Models. Open Science Repository Economics Online, e70081922 (2013).
doi
Research registered in the DOI resolution system as: 10.7392/Economics.70081922.

This work is licensed under a Creative Commons Attribution 3.0 Unported License.