Open Science Repository Computer and Information Sciences

doi: 10.7392/openaccess.70081951

Application of Quantum Evolutionary Algorithm to Complex Timetabling Problem

Jyoti Chaturvedi

Department of Mathematics, Faculty of Science, Dayalbagh Educational Institute, Dayalbagh, Agra, U.P. -282005, India

Abstract

Organizations like universities and schools use timetables to schedule lectures and lab sessions in a way that makes best use of resources available. Making a good timetable is a scheduling problem. It is NP-hard, multi-constrained, complex and a combinatorial optimization problem. The solution of this problem cannot be obtained in polynomial time. Therefore, this problem has captured great attention of researchers for last more than four decades.

Researchers have tried to develop an automated system to solve this problem using various heuristics (e.g. Graph Colouring etc.), local search techniques (e.g. Simulated Annealing and Tabu Search) etc. Some researchers have also employed Evolutionary Algorithms (mainly Genetic Algorithms and its variants) which is a good technique for solving complex problems having very large search space. This paper implements a novel quantum evolutionary algorithm(QEA) to solve the time tabling problem of Dayalbagh Educational Institute (Deemed University). 

Keywords: scheduling problem, evolutionary algorithm, quantum evolutionary algorithm.

I. Introduction

The scheduling of courses in universities or institutions is known to be a highly constrained combinatorial optimization problem. Generally it is done manually. Solution of this problem usually involves taking the previous year’s timetable and modifying that so it will work for the next year. Nowadays most of good universities provide much greater flexibility to students for selecting courses as well as greater choices. Also universities are enrolling more students into a wider variety of courses including an increasing number of combined degree courses. Therefore the process of finding a timeslot for each course so that no two subjects of any student clash has been shown to be equivalent to assigning colours to vertices in a graph so that adjacent vertices always have different colours. This has been proved to lie in the set of NP-complete problems, which means that carrying out an exhaustive search for the timetable is not possible in a reasonable time. Hence there should be some automatic timetabling system, which creates timetable every year [1]. Many course-timetabling algorithms have been proposed. The most popular methods that have and are being introduced for such a system are based on heuristics (e.g. graph colouring etc.), local search techniques (e.g. simulated annealing, tabu search). Some researchers have also employed evolutionary algorithms (mainly genetic algorithms and its variants) and got good solutions. Due to the complexity, the general genetic algorithm converges slowly and easily converges to local optima. A novel quantum-inspired evolutionary algorithms (QEA) has been implemented for the Course Timetable Problem (CTP). The QEA uses genetic operators on the Q-bit as well as updating operator of quantum gate which is introduced as a variation operator to drive the individuals toward better solutions. 

In this work we have implemented Quantum Evolutionary Algorithm for the Timetable Problem. The experimental results demonstrate that the QEA performs well and can also provide a set of high quality timetables.

II. Timetable problem

Timetable problem deals with construction of timetable of the courses. Timetable construction can be considered as generic scheduling activity. The scheduling problems are essentially problems that deal with effective distribution of resources among tasks. 

University Timetable problem also presents a set of tasks (classes) and a set of resources (rooms, Labs, groups, instructors). Every task requests some resources for its realization on certain time slot. The goal is to make the timetable at least as good as experienced human (expert) would make it while satisfying the required constraints. Though each university may have different constraints, two types of constraints are commonly considered [4]: 

a) Hard constraints which must be satisfied in a timetable in order to make it usable (feasible).

b) Soft constraints which are desired but not absolutely essential. Soft constraints are those that are set by the user to produce a timetable that is more suited to their preferences. In other words, violation of only soft constraints means that a valid solution was produced, but only with less quality, depending on the frequency of soft constraint violations.

Some of the hard constraints for timetable problem are given here:

• A student should have only one class at a time. 
• A teacher should have only one class at a time.
• A room should be booked for only one class at a time.
• Only one class of a course should be scheduled on a day.

Some of the soft constraints for timetable problems are given here:

• Student should not have any free time slot between two classes on a day.
• Classes of a teacher should be well spread over the week.
• A smaller class should not be scheduled in a room which can be used for a bigger class.
• Two or more number of classes should not be allotted to a teacher in a day.
• A class should be scheduled only in a specific room, if required, otherwise in a general room which has sufficient sitting capacity for the students of the class.
• A class should be scheduled only at a specific timeslot, if required.

A feasible timetable is one that does not violate any of the hard constraints. On the other hand, a “good” timetable is one that satisfies all hard constraints as well as a number of the soft constraints (or all if possible).

Making a valid timetable is not an easy task. The reason is that it is NP hard. Consider that there are ‘t’ periods and ‘c’ classes to be scheduled then there are t^c ways to do this. It increases exponentially when number of classes increase. Hence, time to finding the solution also increases exponentially. Therefore, we try to reach nearly optimal solution to this problem.

A time and computational saving idea that is adopted in this work is to split the complete timetabling problem into two phases: time (day and hour) allocation and place (classroom) allocation . The assumption is that, after obtaining a solution to the first phase, the second phase is much easier to solve, i.e. there are many solutions to the second phase that satisfy the first phase. The first phase is the most important and difficult one. The constraints are much stronger and the computation effort is much higher in this first phase. After finding a suitable schedule, the allocation of the rooms is a conceptually similar task with the first phase and consequently it can be solved in the same way. The argument behind this separation is that from the search space for n activities, each with a starting time ranging from 0 to m−1, and an allocated room, ranging from 0 to p−1, i.e. an overall search space of mⁿ×pⁿ possible solutions, the two-phase approach will derive a search space of mⁿ + pⁿ possible solutions. This intuitive approach brings obviously an important improvement in the speed and effort of computation of any solving algorithm [3].

III. Evolutionary algorithm

Evolutionary algorithms are the algorithms which are inspired by the famous principle of “Darwinian Evolution Theory”. These algorithms are a very impressive tool to solve complex combinatorial optimization problems. They generally only involve techniques implementing mechanisms inspired by biological evolution.

Candidate solutions to the optimization problem play the role of individuals in a population, and the cost function determines the environment within which the solutions "live". Evolution of the population then takes place after the repeated application of the above operators.

Recombination and mutation create the necessary diversity and thereby facilitate novelty, while selection acts as a force increasing quality. The net effect of survival of the fittest is that the average fitness of the population increases with each generation.

IV. Quantum evolutionary algorithm

Evolutionary algorithms (EAs) are characterized by the representation of the individual, the evaluation function representing the fitness level of the individuals, and the population dynamics such as population size, variation operators, parent selection, reproduction etc. To have a good balance between exploration of search space and exploitation of best solution, these components should be designed properly. Quantum evolutionary algorithm (QEA) can treat the balance between exploration and exploitation very easily. Also, QEA can explore the search space with a smaller number of individuals and exploit the search space for a global solution within a short span of time.

A. Q-bit & Q-bit individual

Q-bit or quantum bit is the smallest unit of information in QEA. It is represented as a pair of numbers (α,β), where |α|² + |β|² = 1. |α|² gives the probability that qubit is found in 0 state and |β|² is the probability that qubit is found in 1 state. A Q-bit may also be in a linear superposition of the two states. A Q-bit individual as a string of m Q-bits is defined as

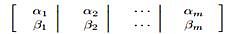
Where |α|²+ |β|²=1, for i=1,2,...m.

Qubit representation has the advantage that it is able to represent a linear superposition of states. If there is for instance, a three qubit system with three pairs of amplitudes, then it contains the information of eight classical states.

B. Population

QEA maintains a population of qubit individuals Q(t)={q^t₁, q^t₂,…….., q^t_n} at generation t, where n is the size of population, and q^t_j is a Q-bit individual defined as

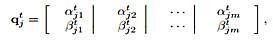
Where m is the number of Q-bits, i.e., the string length of the Q-bit individual, and j = 1, 2, ……, n.

Using qubit individual population we can generate binary population.

C. Quantum rotation gate

Q-bit individuals in Q(t) are updated by applying Q-gates defined as a variation operator of QEA, by which operation the updated Q-bit should satisfy the normalization condition, |α’|²+ |β’|²=1, where α’ and β’ are the values of the updated Q-bit. The following rotation gate is used as a basic Q-gate in QEA:

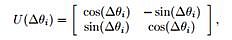
Where ∆Ѳ_i, i = 1, 2……,m, is a rotation angle of each Q-bit toward either 0 or 1 state depending on its sign.

D. Migration

A migration in QEA is defined as the process of copying current best solution in binary population in place of previous solutions. A local migration is implemented by replacing some of the solution in the best individual’s population, while global migration is implemented by replacing all the solution in best individuals population.

V. Methodology

Here is the description about the implementation of the algorithm to find the solutions of the timetable problem.

A. Representation of solution chromosome

• Quantum chromosome is represented as a two dimensional array with each cell containing the amplitudes of 0 and 1.
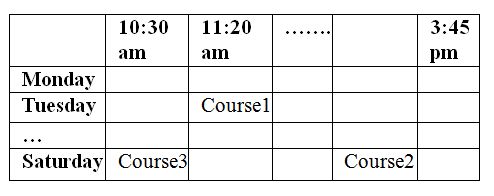
• On the other hand solution chromosome is represented as a two dimensional array having timeslots on horizontal axis and days as on vertical axis as shown below:

• Solution chromosome (i.e course code)  is made up of binary bits.
• Each input given by the user is mapped with some integer value and used as the coded integer value.

B. Evaluation of solution chromosome

Evaluation function or fitness function takes an individual, evaluate its fitness according to the following constraints and return the fitness. The solution is called good or bad solution according to its fitness value. Here more the solution satisfies the constraints, the more it is called fit.

1. Following hard constraints are used in the implementation:

• Each teacher should have only one lecture in one period.
• Each student should have only one lecture in one period.
• Students should have classes on all six days of the week.
• Classes of the subjects from same group (e.g. pm, mc, bz etc.) should not be conducted in parallel.
• Class of a subject should be scheduled in one of the rooms that are assigned to that subject.
• Number of classes of a particular subject in a week should be according to the credit of that subject.
• A room should be scheduled only for one class at a time. 
• Common classes of different years should be scheduled at the same time and same day.
• Classes of core courses should be scheduled in first or last period.
• Teacher’s preferences.
• There should not be more than two classes of a subject on a day.

2. Following soft constraints are used in the implementation:

• Students should have continuous classes in a day.
• There should be gap between two lectures of a teacher.
• Labs should be scheduled in the second half.
• Classes should be best fit (for a room).
• Class of a particular subject should be scheduled in the same room throughout the week.
• Class of a particular subject should be held at the same time throughout the week.

C. Algorithm

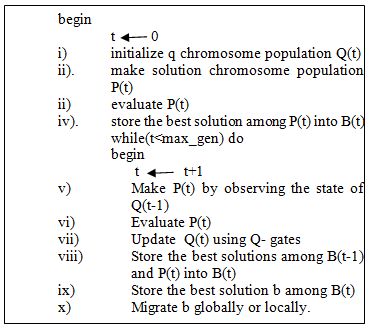
Algorithm shown in figure 2 is used in the implementation. The algorithm contains the following functions:

• Main
• Input
• Make timetable
• Repair
• Fitness
• Update chromosome

Function-make timetable

Formation of the timetable takes place in the function make timetable shown in figure 3.

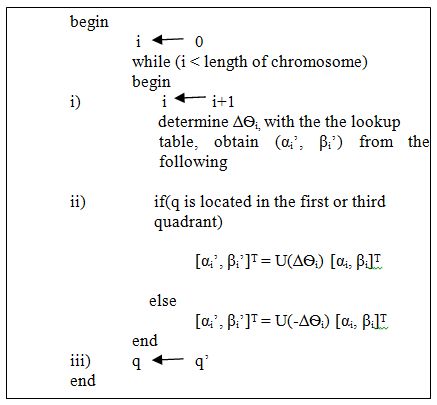
Here quantum chromosomes (i.e all α and β) are intialized with the value 1/√2. Binary solution chromosomes are intialized by observing the states of initial quantum chromosome (i.e. by selecting either 0 or 1 for each bit using the probability of 0 and 1 in quantum chromosome). Initialization is done as shown in figure 4.

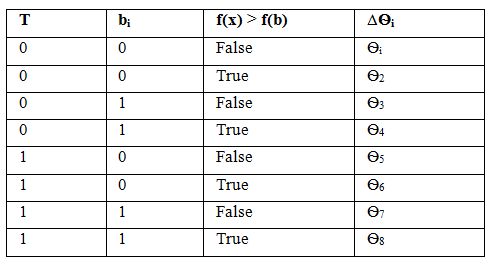
After each iteration Q-chromosome is updated according to the fitness of previous solution chromosome as follows:

Where
Ѳ₁ =Ѳ₂ =Ѳ₄ =Ѳ₆ = Ѳ₇ = Ѳ₈ =0
Ѳ₃ = 0.01π
Ѳ₅ =-0.01π

VI. Results

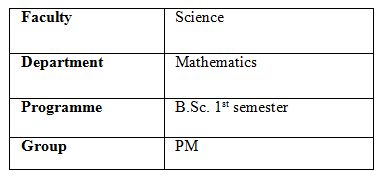
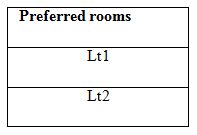
Here  the results obtained from QEA for following input is shown.

Inputs:

Result:

VII. Experimental graphs

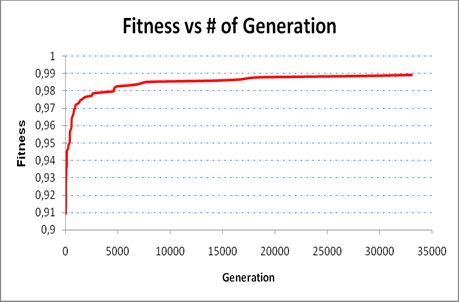
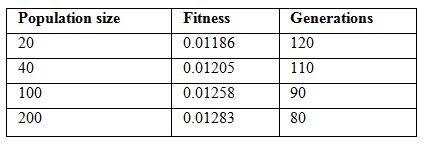
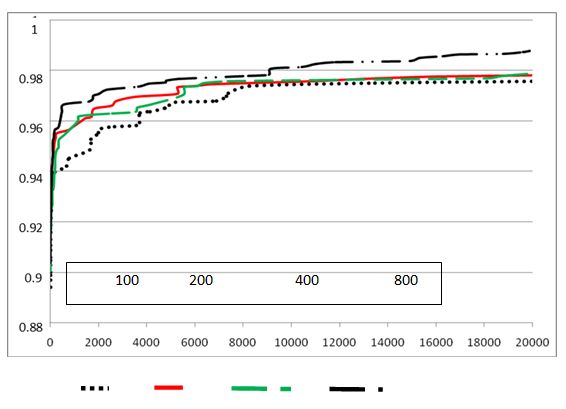
It was seen that the fitness of solution i.e. quality of the timetable increases with the increase in population size and generations.

• The algorithm increases sharply when generation number is between zero and a thousand, however after 5000 generations nearly the same fitness value is observed. Although we reached 30000th generation, we did not get a solution with a fitness value of 1. It is almost impossible that generating timetables which satisfy all individual preferences. 

It can also be seen from the graph shown in the figure below that fitness becomes consistent and doesn’t increase by a large amount after some time. Hence, after some amount of increment in generation fitness becomes consistent.

VIII. Conclusion

The timetable problem is a NP hard problem with various typical hard and soft constraints. In this work, this problem has been solved using quantum inspired Evolutionary Algorithm (QEA). The results show that QEA performs well and gives a good solution.  With the help of QEA, generation of good time table for different courses offered by the Faculties of Dayalbagh Educational Institute, Dayalbagh, Agra after considering many complex hard and soft constraints is possible. 

References

[1] Nilesh Gambhava and Gopi Sanghani, “University Examination Timetabling using Genetic Algorithm”, in proc International Conference on Applied Artificial Intelligence ICAAI’03, Kolhapur, INDIA, Monday, 15th December 2003.

[2] Yu Zheng , Jing-fa Liu ,Wue-hua Geng  and Jing-yu Yang , “Quantum-Inspired Genetic Evolutionary Algorithm for Course Timetabling”, in Proc of 3rd International Conference on Genetic and Evolutionary Computing, 2009. WGEC '09, pp 750 – 753, 14-17 Oct. 2009.

[3]  Liviu Lalescu and Costin Badica, “An Evolutionary Approach for School Timetabling”, in Proc. 14th International Conference on Control Systems and Computer Science, vol. II, pp114,  July 2-5, 2003.

[4] E.K. Burke, J. Kingston and K. Jackson, “Automated university timetabling: the state of the art”, The Computer Journal, Vol. 40, No. 9, pp. 565-571, 1997.

[5] Kuk-Hyun Han and Jong-Hwan Kim , “On the Analysis of the Quantum-inspired Evolutionary Algorithm with a Single Individual”,  in Proceedings of the 2001 International Conference on Artificial Intelligence, July 16-21, 2006.

[6] Kuldeep Kumar, Sikander, Ramesh Sharma AND Kaushal Mehta, “ Genetic Algorithm Approach TO Automate University Timetable”, International Journal of Technical Research(Ijtr), Vol. 1, Issue 1,PP. 33-37, Mar-Apr2012.

 [7] Ho Sung C. Lee, “Timetabling Constrained System via Genetic Algorithm”, Masters Thesis. University of Philippines, Diliman, Quezon City, 2000.

[8] D. Abramson and J. Abela, “A Parallel Genetic Algorithm for Solving the School Timetabling Problem”, in proc.of15 Australian Computer Science Conference, Hobart, pp 1 – 11, Feb 1992.

[9] Rupert Weare, Edmund Burkeand Dave Elliman,“A Hybrid Genetic Algorithm for Highly Constrained Timetabling Problems”, Department of Computer Science University of Nottingham, Nottingham, Technical Report NOTTCS-TR-95-8, 1995.

[10] Liviu Lalescu and Costin Badica, “Timetabling Experiments Using Genetic Algorithms”, University of Craiova, Faculty of Control, Computers and Electronics Software Engineering Department, Romania, July 2003.

[11] Branimir Sigl, Marin Golub, Vedran Mornar, ”Solving Timetable Scheduling Problem by Using Genetic Algorithms”, in proc. of 25th Int. Conf.  Information Technology Interfaces IT1, Cavtat, Croatia, pp. 519-524, June 2003.

[12] C. Y. Cheong, K. C. Tan  and B. Veeravalli, “Solving the Exam Timetabling Problem via a Multi-Objective Evolutionary Algorithm – a more general approach”, in Proceedings of the  IEEE Symposium on Computational Intelligence in Scheduling, CI-Sched, Honolulu, HI, USA, pp. 165 – 172, 2007.

[13] M. Al-Betar, A. Khader and T. Gani, “A Harmony Search Algorithm for University Course Timetabling “, in proc. of 7th Intl. Conf. on the Practice and Theory of Automated Timetabling.Montreal, Canada, Aug. 2008.

[14] Kuldeep Singh Sandhu, “ Automating Class Schedule Generation in the Context of a University Timetabling Information System”, Ph.D. Dissertation, Nathan Campus, Griffith University., 21st September 2001.

[15] Kuk-Hyun Han and Jong-Hwan Kim, “Quantum-inspired Evolutionary Algorithm for a Class of Combinatorial Optimization”, IEEE transaction on Evolutionary Computation, Vol. 6, No. 6, December 2002.

Cite this paper

APA

Chaturvedi, J. (2013). Application of Quantum Evolutionary Algorithm to Complex Timetabling Problem. Open Science Repository Computer and Information Sciences, Online(open-access), e70081951. doi:10.7392/openaccess.70081951

MLA

Chaturvedi, Jyoti. “Application of Quantum Evolutionary Algorithm to Complex Timetabling Problem.” Open Science Repository Computer and Information Sciences Online.open-access (2013): e70081951.

Chicago

Chaturvedi, Jyoti. “Application of Quantum Evolutionary Algorithm to Complex Timetabling Problem.” Open Science Repository Computer and Information Sciences Online, no. open-access (April 10, 2013): e70081951. http://www.open-science-repository.com/application-of-quantum-evolutionary-algorithm-to-complex-timetabling-problem.html.

Harvard

Chaturvedi, J., 2013. Application of Quantum Evolutionary Algorithm to Complex Timetabling Problem. Open Science Repository Computer and Information Sciences, Online(open-access), p.e70081951. Available at: http://www.open-science-repository.com/application-of-quantum-evolutionary-algorithm-to-complex-timetabling-problem.html.

Science

1. J. Chaturvedi, Application of Quantum Evolutionary Algorithm to Complex Timetabling Problem, Open Science Repository Computer and Information Sciences Online, e70081951 (2013).

Nature

1. Chaturvedi, J. Application of Quantum Evolutionary Algorithm to Complex Timetabling Problem. Open Science Repository Computer and Information Sciences Online, e70081951 (2013).

doi

Research registered in the DOI resolution system as: 10.7392/openaccess.70081951.

This work is licensed under a Creative Commons Attribution 3.0 Unported License.